Happy Pi Day! Well, maybe this won’t go up until after Pi Day, but it’s currently Pi Day as I write this. To celebrate the occasion, I decided to write about pi types. I figured that this was also a great time to write about my journey towards understanding dependent types. I’m not exactly an expert of type theory and it was difficult even making it this far, but hopefully this post makes it easier for others to reach this point.

What are dependent types?

Dependent types are types whose definitions depend on values. This can be kind of mind-bending, since we typically tend to distinguish types from values in most popular programming languages. In a dependently typed language, types are first-class, meaning they can be used like values. This is quite similar to how functions are first-class in most programming languages (passing functions as arguments to other functions).

Informally, we tend to think of types as sets of values. For example, the values 1, 2, and 3 might be members of the type int. In a dependently typed language, types are members of their own type, which I will call Type. Of course, by the same reasoning used in Russell’s Paradox, we can’t have a set of all sets. Thus, we can’t have a type of all types. Instead, we call the type of types a (type) universe, where the universe of types called Type would be a member of universe Type1, Type1 would be a member of Type2, and so on. This is how languages like Idris avoid the aforementioned paradox problem, although other dependently typed languages (such as Formality) define Type: Type due to differences in their underlying type theories. Again, I should stress that types aren’t actually sets, but this informal view of them is sufficient for understanding the rest of this post.

From the top

In order to build up an intuition for how to reason with dependent types, I will start from plain old Rust functions. Rust does not support dependent types, but I would like to draw some parallels between the more familiar C-style syntax of Rust and Idris’ syntax. In addition, I will be drawing some parallels between Idris’ syntax and predicate logic to help round things out.

Generics

Before we can really dig into this, we’re going to need to have an understanding of how generics work in Rust and other similar languages (such as Java, C#, etc.). We’ll start from the identity function:

fn id<A>(a: A) -> A {
  a
}

As the name suggests, the identity function takes a value of any type A and must return a value of that same type A. Note that we have no other choice but to return the input argument a itself, since there is no magical way for us to conjure up a value of type A from thin air. Our function implementation is driven by our function’s type signature, ignoring the possibility of side-effects. Generics are monomorphized in Rust, meaning that the caller of our id function will choose what type A will be. You can think of this as copying and pasting id with the chosen type replacing all instances of A. For example, if we called id with a value 2u32, our function id will be copied and pasted as follows:

fn id<u32>(a: u32) -> u32 {
  a
}

Rewrite it in… Idris?

At this point, we’re ready to try implementing this function in Idris. For this section, I want to focus on the type signature, since it is easily the most important part of the function’s definition. In Idris, our type signature can be written as follows:

id : a -> a

In Idris, generic type parameters are typically written in lowercase. This syntax is much less verbose than the Rust syntax, but it is also leaving some bits implicit. We can rewrite this signature in explicit form:

id : {a : Type} -> (value : a) -> a

Here, the curly braces mean that our parameter a is implicit. I could just as easily have defined this with round parentheses:

id : (a : Type) -> (value : a) -> a

This means we need to explicity pass a type as an argument to id now.

For those who are unfamiliar with this type signature syntax, this is just a function that takes 2 arguments: a of type Type, and value of type a. Remember, types are first-class in Idris! You’ll notice that we have two arrows in the signature instead of splitting the arguments with a comma. Idris supports currying, which means that we can view this function as taking an argument a of type Type and returning a function which takes a value of type a and returns a value of type a. In other words, we can partially apply the function by supplying each argument one at a time instead of giving all of the arguments up front. More formally, we could state that the function type a -> b -> c is isomorphic to the function type (a, b) -> c.

Let’s compare our two syntaxes now:

// Rust
fn id<A>(a: A) -> A

// Idris
id : {a : Type} -> (value : a) -> a

To avoid confusion, I renamed the Rust parameter a as value in the Idris example. As you can see, the <A> of Rust’s C-style syntax specifies that A is indeed a type parameter, not just a value parameter. In Idris, that distinction in syntax disappears as types are treated just like regular values.

Idris to Predicate Logic

Now, we will make use of a result known as the Curry-Howard correspondence/isomorphism. What Curry-Howard states is that there exists a transformation from types to logical propositions and from logical propositions back into types. This may sound kind of crazy, but it’s true! However, this mapping only works for languages like Idris that do not support infinite loops or exception throwing (basically, any function that doesn’t return a value). Okay, technically, Idris DOES allow infinite recursion, but Idris has a termination checker that can tell you if your program definitely terminates. Only terminating programs correspond to logical proofs.

Note that Idris’ termination checker isn’t a solution to the halting problem, which states that termination is an undecidable property. By undecidable, I mean that given an arbitrary program, Idris can’t answer “Yes” or “No” to the question “Does this program terminate?”. Instead, Idris’ termination checker makes a conservative guess about whether or not an arbitrary program terminates. This means that for some programs that do terminate, the termination checker might say “I don’t know if this program terminates or not”.

Without further ado, I’m going to show an equivalent definition of the Idris function in predicate logic, which we will subsequently break down:

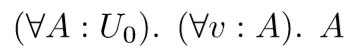
U0 is the first type universe, which contains all types.

In Rust and Idris, we read a : A as ”a is of type A“. In our logical interpretation, we can read this as ”a is a proof of the proposition A” by Curry-Howard. In fact, we could say that any implementation of our function id that compiles is a proof of this proposition.

We can take this a step further. We can also rewrite this as follows:

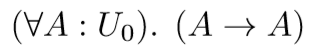
Which we can read as “for all propositions A in universe U0, A implies A“. This has several implications (no pun intended). Already, by using this arrow notation, we are a lot closer to Idris’ function signature syntax, which helps us to see the correspondence. Secondly, it shows that implication is a special case of universal quantification under certain circumstances. I will discuss this second point in more detail later.

Dependent Function Types (pi types)

At this point, we’re ready to look at some dependently typed functions. Here, I define Vect n a as a vector of length n containing objects of type a, just as it is defined in Idris. We will write a function that takes a natural number (that is an integer from 0 to positive infinity) and produces a vector of objects of a given type with that length. Note that Vect is parameterized not only by a type, but by a length, which is a numerical value. Here’s the definition of our function:

// being super explicit here 
mkVect : {a: Type} -> (n : Nat) -> (value : a) -> Vect n a
mkVect Z value = []
mkVect (S n) value = value :: mkVect n

// implicit version
mkVect : (n : Nat) -> a -> Vect n a

We can mostly ignore the function’s implementation. It simply produces a vector of length n where all the elements are some value of type a. What is important here is the type signature. We now have a type signature where the return type depends on the argument to the function. How does this look from a more logical perspective?

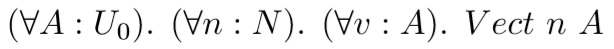
Here, N represents the natural numbers and Vect is a predicate that takes the value variable n and the type variable A. I’m glossing over a few details related to how Vect is defined, but I think we can safely ignore them for the sake of this discussion. What is important to note here is that we reason with both type variables and value variables universally.

Note that we don’t need v at all. Vect is only parameterized by n and A, so we can rewrite this as follows:

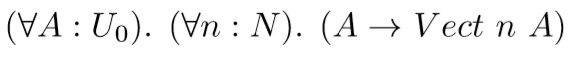
That might seem confusing, but what this is really showing is that you can treat “implies” as a special case of the universal quantifier if the proposition on the right-hand side does NOT depend on the quantified variable.

Okay, so that’s all cool, but how does this work in programming? This is the part that I struggled with the most when comparing dependent types to Rust and its const generics. The first question anyone asks me when I talk about dependent types is “How do you determine what type a value has if it relies on a runtime value?”. Usually, if a program is poorly typed, the compiler will reject it and not allow you to run it. This is confusing in the context of dependently typed languages because many values are determined at runtime, such as user input, but bad programs are rejected at compile-time. It sort of creates a chicken and egg problem, right? Well, it turns out that it doesn’t. By the same reasoning we use for generic type arguments, we can write functions over generic value arguments (you know, the regular ol’ parameters you’ve been using in literally every other language!). This is where our reasoning with universal quantification comes in handy. mkVect takes any arbitrary value n of type Nat, so it doesn’t matter what the value of n is at runtime.

In this case, since the implementation of mkVect is recursive, it corresponds to a proof by induction (the recursive call is our inductive hypothesis). Thus, we can state that we can produce a Vect of any given length n.

Here’s an example of how we might try to monomorphize mkVect:

// We will replace all instance of a and n by the specific types/values we get
mkVect : {a: Type} -> (n : Nat) -> (value : a) -> Vect n a

// Monomorphize using String (Idris probably doesn\'t do this under the hood, but it\'s a good mental model to reason with)
mkVect : {String: Type} -> (n : Nat) -> (value : String) -> Vect n String 

// Here is what this might look like if we gave 3 as the length at compile time.
mkVect : {String: Type} -> (3 : Nat) -> (value : String) -> Vect 3 String 

Note that we cannot define a function that takes a Vect of arbitrary length (such as one we might construct at runtime) and pass it to a function that requires a Vect with a specific length. That would be like trying to pass HashSet<T> to a function that takes HashSet<String>. It won’t type-check, so the program correctly fails to compile in these cases. Despite not knowing the concrete value of the length at compile time, we can still reason with it generically, meaning we have all of the information we need for type checking at compile time. Thus, there’s no case where we will run into a chicken and egg problem. For the cases where you need to provide a specific length Vect and only have a runtime created Vect, then you will need to provide proof that the runtime value has the correct length. As an example, a function with signature Vect n a -> Maybe (Vect 3 a) would allow you to extract a vector of length 3 in cases where n is 3 and would return Nothing otherwise. This is not unlike using a smart constructor.

Why Pi?

Now that I’ve gone through all the trouble of defining what dependent types are and how to reason with them, it’d be nice to know what super-powers they give us, right? First of all, they allow us to more precisely define our data types. For example, Vect being parameterized by its length allows the compiler to check for index out of bounds errors at compile time. In addition, they allow the compiler to more easily perform proof searches, which automatically will implement functions based solely on their function signatures. They also give us the means to formally verify our programs in the same language as we write them in by simply compiling them. I highly recommend checking out Edwin Brady’s book Type-Driven Development with Idris for concrete examples of how to use pi types to solve practical problems.

Comparison with const generics

So what is it about dependent types that separates them from const generics? Well, as the name suggests, const generics require all values to be known at compile-time before they can be used as generic arguments (I can’t really call them type arguments at this point). For example, I can define the following function in Rust:

// A vector of length N containing elements of type A
struct Vect<const N: u32, A> {
    ...
}

fn mkVect<const N: u32>() -> Vect N String

… but I can’t define this one:

// theoretical syntax
fn mkVect(n: u32) -> Vect n String

// alternate theoretical syntax that also doesn't work
fn mkVect<N: u32>() -> Vect N String

Note that in the first example, the value of N must be decided at each call site and must be known strictly at compile time. The second example takes any arbitrary value, which may not be known at compile time. As you can see, dependent types give us a superset of the functionality of const generics by allowing us to generically reason with values only known at runtime.

So, why does Rust not just support full on pi types? It turns out that there was an effort to try and add pi types to Rust once before, but this didn’t pan out, most likely due to breakages in the type system. I personally hope that this is revisited again after const generics are stabilized, but I don’t think it’s too likely that Rust will be seeing pi types any time soon.

About Sigma Types

When people talk about dependent types, they sometimes mention sigma types. Sigma types correspond to existential quantification in logic, so they can be implemented in terms of pi types. Thus, if you can use pi types, you should be able to define your own sigma types.

Closing

Phew! There you have it! That’s pretty much everything I know about dependent types at the moment. If there’s anything wrong in there, please let me know and I’ll amend it. Thanks for reading!